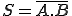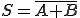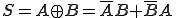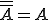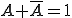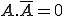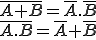Table des matières
Fonctions logiques
Définition
Variable logique: C'est une grandeur représentée par un symbole qui peut prendre les valeurs 0 et 1 suivant certaines conditions.
Fonction logique: Groupe de variables reliées par des opérateurs logiques
Table de vérité:
n entrées → 2n combinaisons
| entrées | sorties | |
|---|---|---|
| A | B | S |
| 0 | 0 | x |
| 0 | 1 | x |
| 1 | 0 | x |
| 1 | 1 | x |
Variable logique: 1 ou 0
logique positive:
| niveau logique | |
| 0 | 0V (bas) |
| 1 | 5V (haut) |
logique négative:
| niveau logique | |
| 0 | 5V (haut) |
| 1 | 0V (bas) |
Fonctions logiques élémentaires
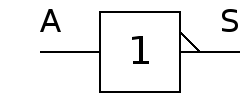
Fonction NON (NOT)
Table de vérité
| A | S |
|---|---|
| 0 | 1 |
| 1 | 0 |
Equation logique
Symbole
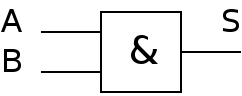
Fonction ET (AND)
Table de vérité
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Remarque: Il faut que les 2 entrées soient à 1 pour avoir la sortie à 1.
Equation logique
Symbole
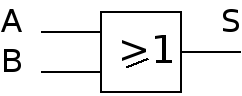
Fonction OU (OR)
Table de vérité
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Remarque: Il suffit qu'une entrée soit à 1 pour avoir la sortie à 1.
Equation logique
Symbole
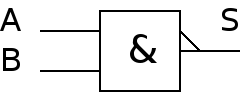
Fonction NON ET (NAND)
Table de vérité
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Equation logique
Symbole
Fonction NON OU (NOR)
Table de vérité
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Equation logique
Symbole
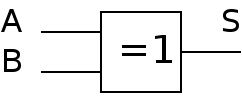
Fonction OU EXCLUSIF (XOR)
Table de vérité
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Equation logique
Symbole
Propriétés des fonctions logiques
Element neutre
A+0=A A.1=A A+1=A
Commutativité
A+B=B+A A.C=C.A
Associativité
A+B+C=(A+B)+C
Distributivité
A.(B+C)=A.B+A.C
Complèment
Théorème de Morgan
Simplification avec un tableau de Karnaugh
La méthode de Karnaugt permet la simplification graphique d'une fonction.
Table de vérité du système
| A | B | C | D | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0(1) |
| 0 | 0 | 0 | 1 | 1(2) |
| 0 | 0 | 1 | 0 | 0 |
| . | . | . | . | . |
| . | . | . | . | . |
| . | . | . | . | . |
| . | . | . | . | . |
Tableau de Karnaugh
| /A,/B (0,0) | /A,B (0,1) | A,B (1,1) | A,/B (1,0) | |
|---|---|---|---|---|
| /C,/D (0,0) | 0(1) | 1 | 1 | 0 |
| /C,D (0,1) | 1(2) | 1 | 0 | 1 |
| C,D (1,1) | 0 | 1 | 0 | 1 |
| C,/D (1,0) | 0 | 1 | 0 | 0 |
Règle 1: On ne peut regrouper qu'un nombre de case correspondant à une puissance de 2 (2,4,8 etc cases)
Règle 2: Le groupement des cases doit être en ligne, en carré ou en colonne
Règle 3: La taille du groupement et le nombre variables sont liés.
Règle 4: Il faut utiliser tous les “1” au moins une fois dans tous les groupements
Règles 5: Pour obtenir une expression simplifié. Il faut chercher les groupements les plus grands et chercher les groupements par les cases qui n'ont qu'une facon de se grouper.
Un groupement est un produit de termes qui ne change pas. La sortie “S” est la somme les groupements.
S=/A.B+A./B.D+/A./C.D+/B.C./D