Table des matières
Codage
Introduction
Tout nombre entier peut être représenté dans un système numérique de base “a” avec :
N=n0.a0+n1.a1+…+nn.an
Exemple en base 10, a = 10
137=7.100+3.101+1.102
Numération
Système décimal - Base 10
Symbole {0,1,2…9}
Utilisé dans la vie courante
Système binaire - Base 2
Symbole {0,1}
Utilisé par les électroniciens.
Dans le système binaire, le bit de poids le plus faible s'appelle LSB (least significant bit). Il est représenté par le bit le plus à droite. Inversement pour le MSB (most significant bit).
| bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
|---|---|---|---|---|---|---|---|
| MSB | LSB | ||||||
Système octale - Base 8
Symbole {0,1,2…7}
Ce système a été utilisé à une certaine époque dans les calculateurs.
Système héxadécimal - Base 16
Symbole Symbole {0,1,2…9,A,B,C,D,E,F}
Utilisé par les électroniciens.
C'est le système le plus utilisé dans les systèmes travaillant avec des nombres multiples de 4 bits: micro pocesseur, micro ordinateur etc ..
Conversion
Base 2 > Base 10
(1010)2
| 1 | 0 | 1 | 0 |
|---|---|---|---|
| 1×23 | 0x22 | 1×21 | 0x20 |
| 8 | 0 | 2 | 0 |
8+0+2+0=10
(1010)2=(10)10
Base 8 > Base 10
(137)8
| 1 | 3 | 7 |
|---|---|---|
| 1×82 | 3×81 | 7×80 |
(137)8=(95)10
Base 16 > Base 10
(5EF)16 on écrit aussi 5EFH
| 5 | E | F |
|---|---|---|
| 5×162 | 14×161 | 15×160 |
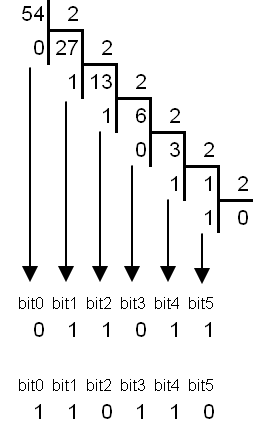
Base 10 > Base 2
(54)10
On divise 54 par 2 jusqu'à avoir un résultat nul. Si le reste de la division est nul on écrit 0, s'il ne l'est pas on écrit 1.
(54)10=(110110)2
Base 2 > Base 16
(110110)2
On fait des groupements de 4 bits
(110110)2 = (0011 0110)2
On convertit en décimal chaque groupement de 4 bits
(0011)2 = (3)10
(0110)2 = (6)10
Au final :
(110110)2=(36)10
Représentation des nombres
Il faut distinguer des nombres signés et non-signés. Dans le cas des nombres signés le module tient compte de tous les bits.
Représentation signe + module
| Signe | module | |||
Signe = 0 → nombre positif
Signe = 1 → nombre négatif
Inconvénient, il y a 2 représentations différentes pour le 0:
+0 : 00 -0 : 10
Cette représentation n'est pas utilisée.
Représentation en complément
On complémente la valeur binaire de 5 et on lui rajoute 1.
| 5 | 0101 |
|---|---|
| /N | 1010 |
| /N+1 | 1011 |
(1011)2 = (-5)10
Exemples:
(01110)2 = (14)10 en signé et en non-signé
(10111)2 = (-7)10 en signé et (23)10 en non-signé
Codage
Code ASCII
Le code ASCII
Code BCD ( Binary Coded decimal )
Codage utilisé pour l'utilisation d'afficheurs 7 segments.
Code Gray ou binaire réfléchi
Il n'y qu'un bit qui change lors de la transition d'un code au suivant
| 0000 |
| 0001 |
| 0011 |
| 0010 |
| 0110 |
| 0111 |
| 0101 |
| 0100 |
| 1100 |
| 1101 |
| 1111 |
| 1110 |
| 1010 |
| 1011 |
| 1001 |
| 1000 |
Applications : Codeurs optique ou tableau de Karnaugh